A segunda lei da radioatividade foi proposta pelo químico Frederick Soddy e está relacionada com a liberação de partículas (ou radiação) beta (β) a partir do núcleo de um átomo qualquer.
Assim como foi definido na primeira lei da radioatividade, a segunda lei da radioatividade também aborda a transformação de um núcleo atômico em outro, porém esse processo ocorre por meio da emissão de partícula beta, que apresenta número de massa igual a 0 e número atômico igual a -1.
Em seus estudos, Soddy percebeu que, toda vez que um núcleo radioativo emite uma partícula beta, forma um novo núcleo com o mesmo número de massa do anterior e número atômico uma unidade maior, como podemos observar na equação nuclear geral abaixo:
ZXA → Z+1DA + -1β0
-
Para o número de massa:
Se igualamos o número de massa do átomo inicial com a somatória das massas nos produtos da equação, confirmamos que a massa desse átomo não se altera:
A = A + 0
A = A
-
Para o número atômico:
Se igualarmos o número atômico do átomo inicial com a somatória dos números atômicos nos produtos da equação, confirmaremos que ocorre o aumento de uma unidade:
Z = Z+1 + (-1)
Z = Z + 1
Essa alteração pode ser melhor percebida em um exemplo real de ocorrência da segunda lei da radioatividade, como na transformação do carbono em nitrogênio na atmosfera:
6C14 → 6+1N14 + -1β0
6C14 → 7N14 + -1β0
Como é possível observar no exemplo acima, de acordo com a segunda lei da radioatividade, a emissão de radiação beta faz o número atômico do átomo aumentar, porém, para que isso ocorra, é necessário um aumento no número de prótons. Como isso seria possível?
Essa dúvida foi resolvida apenas quando o físico italiano Enrico Fermi propôs uma hipótese para desvendar esse mistério, que foi chamada de hipótese de Fermi. De acordo com essa teoria, em um núcleo instável que emite radiação beta, um nêutron (n) sofre uma transformação, cuja motivação ainda desconhecida:
0n1 → -1β0 + 1p1 + 0ν0 (neutrino)
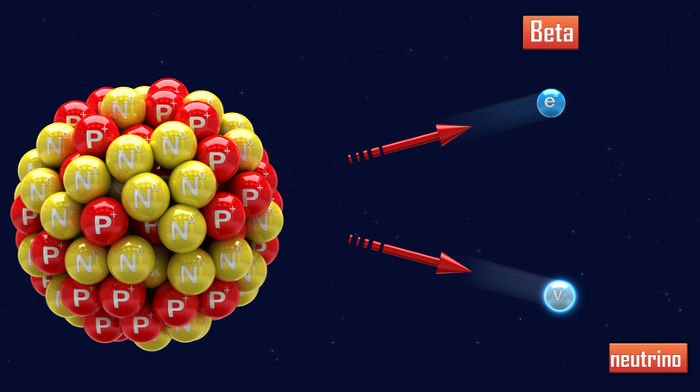
Representação da emissão de uma radiação beta
Nesse processo, o nêutron transforma-se em três novas partículas: a radiação beta (que é um elétron), um próton e um neutrino (que é um nêutron de menor tamanho). Dessas três, beta e neutrino saem do núcleo por não apresentarem massa, e o próton permanece em seu interior, ampliando, assim, o número de prótons presente nesse átomo.
Confira agora alguns exemplos de aplicação da segunda lei da radioatividade:
1º Exemplo - (UFSCar-SP) O aumento no volume das exportações no Brasil, em 2004, tem sido apontado como um dos responsáveis pela retomada do crescimento econômico do país. O Brasil exporta muitos tipos de minérios, sendo que alguns apresentam radioatividade natural. Certos países compradores exigem um certificado apresentando os valores de atividade de átomos que emitem radiação gama. O potássio-40, radioisótopo natural, é um dos emissores dessa radiação. No decaimento radiativo do potássio-40, em geral, há a emissão de uma partícula beta negativa. Nesse caso, resulta em um elemento com número atômico igual a:
a) 40.
b) 39.
c) 21.
d) 20.
e) 19.
Analisando a tabela periódica, é possível notar que o potássio possui número atômico 19. O enunciado indica que esse elemento emite uma partícula beta e forma um novo elemento. Portanto, seu novo número atômico é igual a 20, pois, sempre que um átomo emite radiação beta, o número atômico aumenta em uma unidade.
2º Exemplo - (Unifap-AP) A desintegração radioativa natural do 89Ac227 leva à emissão de uma partícula β (beta) e um átomo de:
a) 89Th228.
b) 88Th227.
c) 88Ra224.
d) 88Ra226.
e) 90Th227.
Quando o átomo de actínio emite radiação beta, gera um novo elemento de mesmo número de massa, isto é, 227, e número atômico uma unidade maior, portanto, igual a 90. Então, nesse exemplo, ocorre a transformação do actínio em tório.
