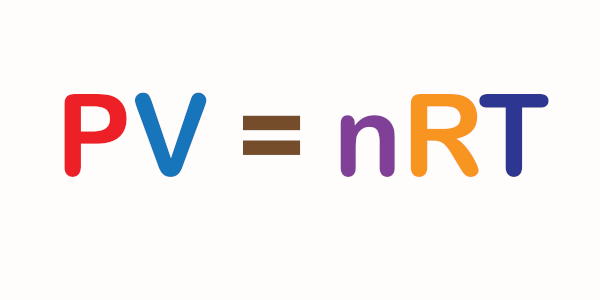Pressão parcial dos gases
A pressão parcial dos gases, também chamada de Lei de Dalton, é a força que os gases exercem sobre os componentes de uma mistura gasosa.
Por Diogo Lopes Dias

PUBLICIDADE
No ano de 1801, o cientista inglês John Dalton publicou suas conclusões sobre experimentos relacionados com fenômenos meteorológicos e com a composição do ar atmosférico. Entre essas conclusões está a definição de pressão parcial dos gases ou, simplesmente, Lei de Dalton.
A lei da pressão parcial dos gases diz que a pressão total (Pt) que uma mistura de gases (A, B, C) exerce nas paredes de um recipiente é igual à soma das pressões parciais (PA, PB, PC) de cada um dos gases que a compõem:
Pt = PA + PB + PC
Se temos uma mistura gasosa formada por gás oxigênio (O2), gás nitrogênio (N2) e gás metano (CH4), por exemplo, a pressão que essa mistura exerce é a soma das pressões parciais de cada gás:
Pt = PO2 + PN2 + PCH4
Definição de pressão parcial de um gás
John Dalton, em suas experiências, percebeu que a pressão que um gás presente em uma mistura gasosa exerce nas paredes de um recipiente é igual à pressão que ele exerce sozinho nas paredes de outro recipiente, isto é, sem estar misturado com outro gás. Porém, essa avaliação só ocorre se tivermos o mesmo volume e a mesma temperatura.
A descrição proposta acima é a definição de pressão parcial de um gás, mas para facilitar o entendimento sobre esse assunto, vamos utilizar as duas situações abaixo para o gás carbônico (CO2)
-
Situação 1
Recipiente com um volume de 2 L de gás carbônico a 300 Kelvin:
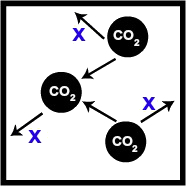
Recipiente com certo volume de CO2
Na representação, podemos observar que as moléculas de CO2 chocam-se com as paredes do recipiente e com as outras moléculas. Esse choque gera uma pressão que vamos chamar de x. Logo, a pressão parcial do CO2 é igual a x.
-
Situação 2
Recipiente com 2L de mistura gasosa, a 300 K, na qual o gás carbônico é um dos gases:
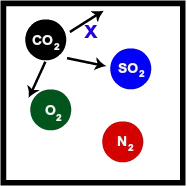
Recipiente contendo uma mistura gasosa com CO2
Na representação, observamos que as moléculas de CO2 também se chocam com as paredes do recipiente com as outras moléculas. Por apresentar mesmo volume (mesmo que contendo gases diferentes) e mesma temperatura, a pressão que o CO2 gera também será x.
Pressão parcial dos gases e a equação de Clapeyron
A equação de Clapeyron é:
PV = nRT
P é a pressão de um gás; V, o volume; n, número de mol; R, constante geral dos gases; e T, a temperatura. Como a pressão total é a soma das pressões de cada gás, podemos também somar a quantidade de matéria deles, já que na mistura os gases estão ocupando o mesmo espaço:
nt = nA + nB + nC
Assim, como o volume, constante (R) e a temperatura a que a mistura gasosa é submetida são sempre constantes, temos que:
Pt = nt
Podemos perceber que a pressão é dependente da quantidade de matéria (n) de um gás. Por isso, podemos relacionar a pressão parcial de um gás com a pressão parcial total de uma mistura, realizando o mesmo procedimento com a quantidade de matéria, resultando na seguinte fórmula:
Pgás = ngás
Pt nt
Como a divisão entre o número de mol de um material pelo número de mol total é denominada de fração em quantidade de matéria, podemos escrever a expressão para calcular a pressão parcial de um gás da seguinte maneira:
Pgás = Xgás
Pt
Cálculos envolvendo pressão parcial dos gases
Exemplo 1: Um recipiente com capacidade igual a 30 litros apresenta uma mistura gasosa contendo 0,5 mol de O2, 1,5 mol de N2 e 2 mol de CO2, a 350 Kelvin. Sabendo que R (constante geral dos gases) vale 0,082 atm.L.mol-1.K-1, qual será a pressão parcial de cada gás na mistura?
Os dados fornecidos pelo exercício foram:
nO2 = 0,5 mol
nN2 = 1,5 mol
nCO2 = 2 mol
R = 0,082 atm.L.mol-1.K-1
T = 350 K
V = 30 Litros
Como é solicitada a pressão parcial de cada gás, é necessário conhecer a pressão total da mistura. É possível calcular a pressão total porque conhecemos o volume, a temperatura e temos o número de mol de todos os gases. Dessa forma, basta utilizar a equação de Clapeyron da seguinte maneira:
Pt.V = nt.R.T
Pt.V = (nO2 + nN2 + nCO2).R.T
Pt.30 = (0,5 + 1,5 +2). 0,082.350
Pt.30 = 4.0,082.350
Pt.30 = 114,8
Pt. = 114,8
30
Pt. = 3,82 atm
Conhecendo a pressão total e sabendo que a soma do número de mol dos gases (nO2 + nN2 + nCO2) é 4 mol, basta utilizar a expressão para cálculo da pressão parcial de cada gás:
-
Para o O2:
PO2 = nO2
Pt nt
PO2 = 0,5
3,82 4
4.PO2 = 3,82.0,5
PO2 = 1,91
4
PO2 = 0,48 atm
-
Para o N2:
PN2 = nN2
Pt nt
PN2 = 1,5
3,82 4
4.PN2 = 3,82.1,5
PN2 = 5,73
4
PN2 = 1,43 atm
-
Para o CO2:
PCO2 = nCO2
Pt nt
PCO2 = 0,5
3,82 4
4.PCO2 = 3,82.2
PCO2 = 7,64
4
PCO2 = 1,91 atm
Exemplo 2: (UNIFENAS) Qual é a pressão parcial de oxigênio que chega aos pulmões de um indivíduo quando o ar inspirado está sob pressão de 740 mmHg? Admita que o ar contém 20% de oxigênio (O2), 78% de nitrogênio (N2) e 2% de argônio (Ar) em mols.
a) 7,4 mmHg
b) 148,0 mmHg
c) 462,5 mmHg
d) 577,0 mmHg
e) 740,0 mmHg
Os dados fornecidos pelo exercício foram:
Pt = 740 mmHg
porcentagem de O2 = 20% (dividindo por 100, temos a fração molar, X, do O2)
XO2 = 0,2
porcentagem de N2 = 78% (dividindo por 100, temos a fração molar, X, do N2)
XN2 = 0,78
porcentagem de Ar = 2%
(dividindo por 100, temos a fração molar, X, do Ar)
XAr = 0,02
PO2 = ?
Como temos a pressão parcial do ar e a fração molar do gás oxigênio, basta utilizar a seguinte relação para encontrar a pressão parcial do O2:
PO2 = XO2
Pt
PO2 = 0,2
740
PO2 = 0,2
740
PO2 = 740.0,2
PO2 = 148 mmHg
Por Me. Diogo Lopes Dias