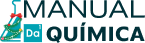Estequiometria

Estequiometria é uma área fundamental da química que quantifica as relações entre reagentes e produtos em reações químicas. Isso ajuda a entender as proporções moleculares e as quantidades de massa envolvidas nas transformações químicas. Ao analisar as proporções atômicas e moleculares em uma reação, a estequiometria permite antecipar e controlar com precisão as quantidades de substâncias envolvidas, sendo uma ferramenta necessária em laboratórios, indústrias e até mesmo em atividades cotidianas.

Leia também: Massa molar e número de mol — entenda conceitos e diferenças

Resumo sobre estequiometria

• A estequiometria é um ramo da Química que estuda as relações quantitativas entre reagentes e produtos em reações químicas.
• Ela utiliza cálculos para determinar as proporções de massa, a quantidade de moléculas e outros parâmetros envolvidos em uma reação.
• As leis das proporções definidas, da conservação das massas e das proporções múltiplas servem como tripé para a compreensão das relações estequiométricas.
• Na estequiometria, a massa molar é utilizada para conversão entre unidades de massa e mols.
• As relações estequiométricas podem ser do tipo mol-mol, massa-massa, mol-massa, mol-número de moléculas.
• Exemplos práticos incluem a queima de combustíveis e a produção industrial de produtos químicos.

Videoaula sobre estequiometria

O que é estequiometria?

A estequiometria é um ramo da Química que estuda as relações quantitativas entre os reagentes e produtos em uma reação química. Portanto, ela analisa as proporções de átomos, moléculas e massas envolvidas, permitindo compreender a quantidade de substâncias consumidas e produzidas durante uma reação. Funciona basicamente como uma ferramenta de cálculo nas reações químicas.

Por exemplo, na reação de combustão completa de um hidrocarboneto, neste caso o metano (CH₄), sempre haverá a produção de dióxido de carbono (CO₂) e água (H₂O), mas em qual proporção? Isso dependerá da quantidade de mols disponíveis dos nossos reagentes, isto é, tanto do combustível (metano) quanto do comburente (oxigênio), como pode ser visto, a seguir, na equação balanceada:

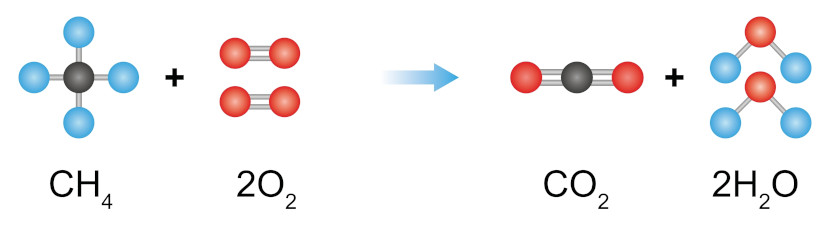
Nessa reação temos uma proporção de 1:2:1:2. Isso significa que, para cada 1 mol de CH₄, são necessário 2 mols de O₂, que produzirão 1 mol de CO₂ e 2 mols de água. Sendo assim, essa proporção nos dá uma noção da estequiometria dessa reação e nos ajuda a compreender tanto a quantidade de reagentes necessários para que a reação aconteça quanto o quantitativo de produto que será formado.

Para que serve a estequiometria?

A estequiometria serve como ferramenta para diversas aplicações práticas, pois vai além do laboratório e entra diretamente em nossas cozinhas e processos industriais. A precisão na dosagem de ingredientes, como seguir uma receita culinária, reflete diretamente a aplicação dos princípios estequiométricos. Ela oferece uma visão detalhada das reações químicas e desempenha um papel fundamental na eficiência dos processos, na economia de recursos e na busca por métodos mais sustentáveis e ambientalmente conscientes.

Veja também: Como fazer o balanceamento de equações químicas

Cálculo da estequiometria

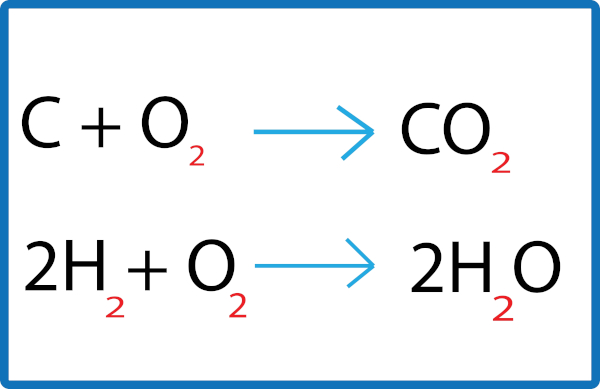
A estequiometria envolve cálculos que relacionam as quantidades de reagentes e produtos em uma reação química. Considerando a lei da conservação das massas, a proporção molar é essencial. Além disso, em algumas ocasiões, será necessário fazer conversão de unidades, uma vez que, em reações químicas, as substâncias têm massa, volume e número de partículas (átomo, moléculas, íons). Diante disso, para facilitar esse processo, dispomos do seguinte diagrama de conversão:

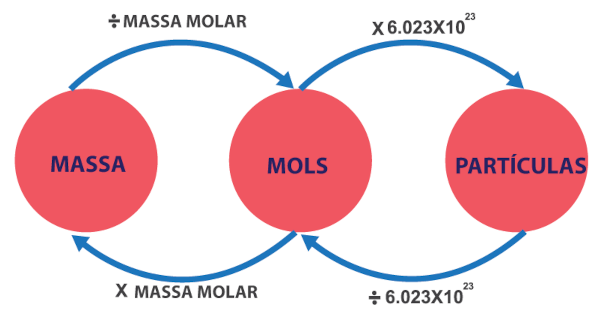
A seguir, vamos explorar possíveis relações estequiométricas, mas vale lembrar que, antes de qualquer cálculo, é necessário estabelecer a equação balanceada da reação. Feito isso, seguiremos para os cálculos.

→ Relação estequiométrica mol-mol

Dada a reação:

2H₂​ + O₂ ​→ 2H₂​O

Quantos mols de O₂​ são necessários para reagir com 8 mols de hidrogênio na formação da água?

Veja que temos a seguinte proporção:

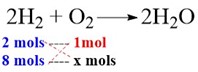
Seguindo a regra de três, temos: x = \(8 \over 2\) = 4 mols.

→ Relação estequiométrica massa-massa

Segue a reação de combustão:

CH₄​ + 2O₂​ → CO₂​ + 2H₂​O

Dados 10 g de CH₄, quantos gramas de CO₂​ serão produzidos?

Usando as massas molares, sabemos que 1 mol de CH₄​ tem 16 g e a massa molar do CO₂​ é 44 g. Portanto, calculamos a massa de CO₂ que será produzida com base em 10 g de CH₄.

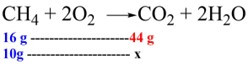
Logo, x = \(440 \over 16\) = 27,5 g de CO₂ serão produzidos.

→ Relação estequiométrica mol-número de moléculas

Tendo em vista a reação de formação da amônia:

N₂ ​+ 3H₂ ​→ 2NH₃​

Dados 2 mols de N₂​, quantas moléculas de NH₃​ serão formadas?

Utilizando a relação molar da reação, sabemos que, para 1 mol de N_2​, formam-se 2 mols de NH₃​, então 2 mols de N₂ produzirão 4 mols de NH_3. Vale lembrar que a quantidade de partículas (átomos, moléculas e íons) é calculada pelo número de Avogadro, em que um mol equivale a 6,02 x 10²³. Portanto:

X = 4 x 6,02 x 10²³ = 24,08 x 10²³ moléculas de NH₃.

→ Relação estequiométrica mol-massa

Dada a reação de formação do óxido de ferro (III):

4Fe + 3O₂ ​→ 2Fe₂​O₃​

Tendo 5 mols de O₂​, qual a massa de Fe₂​O₃​ formada?

Como temos 2 mols de Fe₂​O₃, logo, teremos 2 vezes o valor de sua massa molar: 2 × 159,69 g = 319,38 g. Sabendo que a massa de Fe₂​O₃ é produzida com 3 mols de O₂, temos:

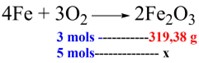
x = \(5x319,38 \over 3\)→ x = \(1.596,9 \over 3\) = 532,3 g de Fe₂​O₃.​

Leis da estequiometria

Como vimos até aqui, a estequiometria determina as proporções necessárias das espécies químicas em uma reação. Contudo, o uso dessa ferramenta é possível graças ao entendimento das leis que governam as reações e que nos ajudam a equacioná-las. São elas:

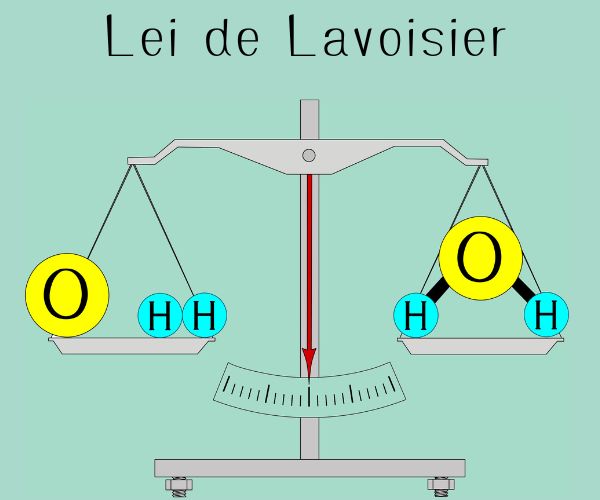
→ Lei da conservação das massas

A massa total dos reagentes é igual à massa total dos produtos em uma reação química, indicando que a matéria não é criada nem destruída.

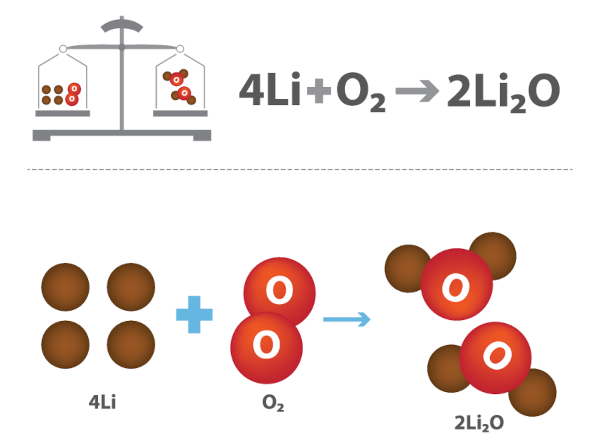
Os átomos de lítio (Li) e oxigênio (O₂) se rearranjam para formar o óxido de lítio (Li₂O), não havendo, portanto, alteração da massa inicial. Para saber mais sobre essa lei, clique aqui.

→ Lei das proporções definidas

Os elementos em um composto estão sempre presentes em proporções fixas e definidas por massa, conforme o exemplo abaixo:

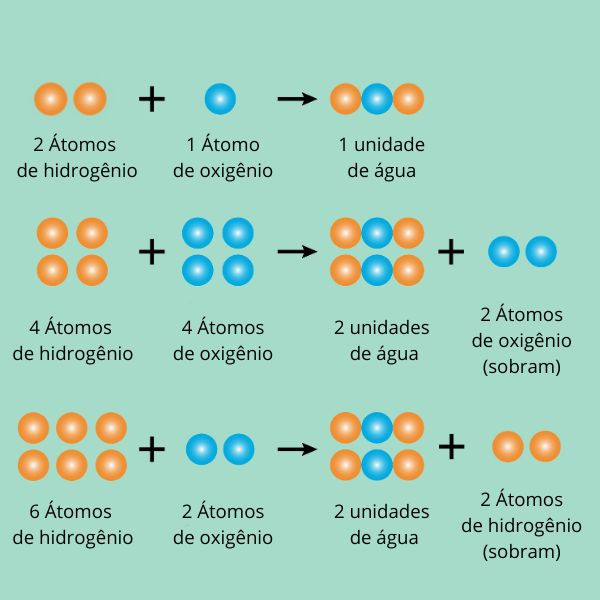
Não importa quantos átomos de oxigênio ou hidrogênio haja a mais, a proporção desses elementos para formar moléculas de água sempre será a mesma, 2:1. Saiba mais sobre essa lei clicando aqui.

→ Lei das proporções múltiplas

Quando dois elementos formam mais de um composto, as massas de um elemento em um dos compostos estão em uma razão de números inteiros simples. Veja os exemplos abaixo:

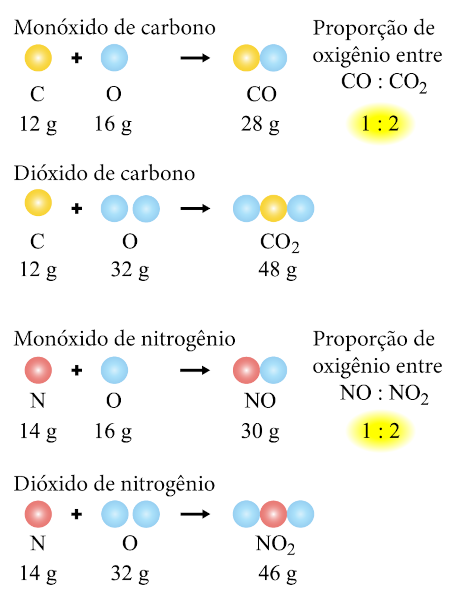
Nesses casos, o oxigênio define as proporções múltiplas ao formar proporções de números inteiros em compostos diferentes com o carbono e o nitrogênio. Perceba que as proporções foram feitas para os átomos de oxigênio, em que, no CO, a proporção é de 16 g, enquanto, no CO₂, é o dobro, ou seja, 32 g. Por isso a proporção de 1:2. De modo análogo, também temos uma proporção de um para 1:2, referente à massa de oxigênio nas moléculas de NO e NO₂.

Essas leis, além de se complementarem, são intrínsecas à compreensão da estequiometria das reações químicas.

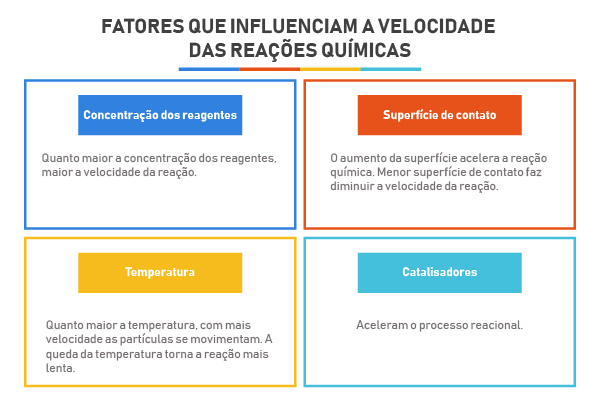
Saiba mais: O que pode influenciar a velocidade de uma reação química?

Aplicação da estequiometria no cotidiano

A estequiometria está presente em diversas situações cotidianas, como cozinhar. Ao seguir uma receita, as proporções corretas de ingredientes são essenciais para garantir que o prato seja preparado com sucesso. Por exemplo, na fabricação de pães, é necessário calcular a quantidade exata de cada ingrediente para produzir uma massa com as características desejadas. Na gastronomia, o conhecimento da relação estequiométrica massa-massa dos ingredientes faz toda diferença no resultado.

Outra aplicação prática é na produção de medicamentos. Para produzir um medicamento, é necessário saber a quantidade exata de cada reagente que será utilizado, e a estequiometria permite calcular essa quantidade de forma precisa, garantindo assim a eficácia do medicamento. Todo medicamento tem uma relação estequiométrica entre o princípio ativo e os excipientes necessários para garantir a eficácia do fármaco.

A estequiometria também é usada na produção de bebidas, como cervejas e refrigerantes. Tanto os sucos industrializados quanto as bebidas alcoólicas apresentam concentrações determinadas por estequiometria. Além disso, a estequiometria é essencial para a compreensão de processos naturais, como a fotossíntese e a respiração celular. A fotossíntese, por exemplo, é um processo que ocorre devido a uma relação estequiométrica entre o CO₂ e H₂O.

Essa área de estudo também é importante para a compreensão de fenômenos como a poluição atmosférica e a mudança climática, permitindo calcular a quantidade de reagentes e produtos envolvidos nesses processos. A estequiometria das emissões de poluentes ajuda no monitoramento da qualidade do ar.

Exercícios resolvidos sobre estequiometria

1. Em um laboratório, um químico planeja realizar a síntese de amônia (NH₃) com base no nitrogênio (N₂) e no hidrogênio (H₂) gasosos. Se 4 mols de nitrogênio reagem completamente com 12 mols de hidrogênio, quantos mols de amônia serão produzidos, considerando a estequiometria da reação?

N₂ ​+ 3H₂ ​→ 2NH₃

A) 2 mols

B) 4 mols

C) 6 mols

D) 8 mols

E) 12 mols

Gabarito: D
A estequiometria da reação indica que 1 mol de N₂ reage para formar 2 mols de NH₃. Portanto, para 4 mols de N₂, resultarão 8 mols de NH₃.

2. Em um experimento, 5 mols de gás hidrogênio (H₂) reagem com excesso de oxigênio (O₂) para formar água (H₂O). Se a estequiometria da reação é respeitada, qual a quantidade de mols de água produzida?

2H₂ ​+ O₂ ​→ 2H₂​O

A) 1 mol

B) 3 mols

C) 5 mols

D) 7 mols

E) 8 mols

Gabarito: C
A estequiometria da reação balanceada indica que 2 mols de H₂ produzem 2 mols de H₂O, ou seja, uma proporção de 1:1. Portanto, para 5 mols de H₂, serão produzidos 5 mols de H₂O.

Fontes

BUSTOS, C. et al. El concepto de equivalente químico y su aplicación en cálculos estequiométricos. Educación Química, v. 18, n. 3, p. 222, 2018.

CHAVEZ, J. DISOLUCIONES QUÍMICAS ESTEQUIOMETRÍA. Revista digital de la Universidad Fermín Toro, v. 4, n. 3, 2017.

GALAGOVSKY, L. R.; DI GIACOMO, M. A.; ALÍ, S. Estequiometría y ley de conservación de la masa: lo que puede ocultar la simplificación del discurso experto. Ciência & Educação (Bauru), v. 21, n. 2, p. 351–360, jun. 2015.

GARCÍA, J. L. G. Algebra de la estequiometría. Educacion Quimica, v. 31, n. 1, p. 138–150, 2020.

L. BROWN, T. et al. Número de Avogadro e mol. In: Química: A Ciência Central. 13. ed. São Paulo: Pearson Education do Brasil., 2016. p. 54–57.

PINTO CAÑÓN, G. Cálculos de estequiometría aplicados a problemas de la realidad cotidiana. Nuevas tendencias en la enseñanza de las ciencias y las ingenierías, v. 1, p. 1–20, 2009.